Once and for all
the idea of glorious victories
won by the glorious army
must be wiped out
Neither side is glorious
On either side they're just frightened men messing their pants
and they all want the same thing
Not to lie under the earth
but to walk upon it
without crutches.
-Peter Weiss, writer, artist, and filmmaker (8 Nov 1916-1982)
When I despair, I remember that all through history, the way of truth and love has always won. There have been murderers and tyrants, and for a time they can seem invincible. But in the end they always fall. Think of it, always.
-Mohandas Karamchand Gandhi (2 Oct 1869-1948)
A king can stand people's fighting, but he can't last long if people start thinking.
-Will Rogers, humorist (4 Nov 1879-1935)
The wisest man is he who does not fancy that he is so at all.
-Nicolas Boileau-Despreaux, poet and critic (1 Nov 1636-1711)
Math Is Still Catching Up to the Mysterious Genius of Srinivasa Ramanujan
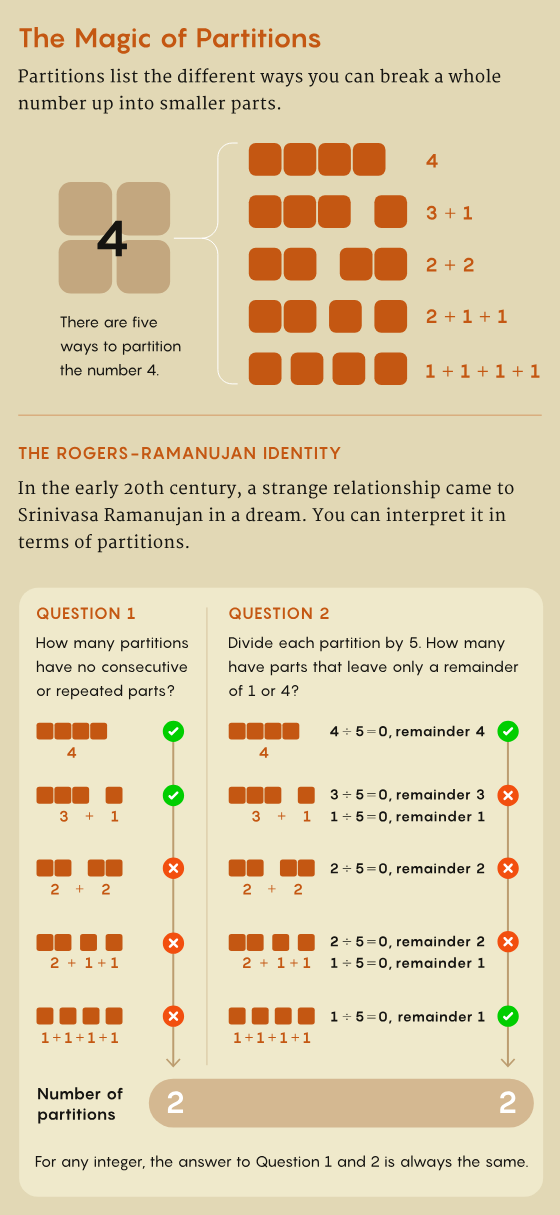
Consider an integer such as the number 4. It can be broken up into parts in a finite number of ways: You can write it as 4, as 3 + 1, as 2 + 2, as 2 + 1 + 1 or as 1 + 1 + 1 + 1. Mathematicians say that the number 4 has five “partitions.” Bigger numbers have far more partitions: The number 200, for instance, has nearly 4 trillion. Partitions are so basic that “people have thought about them as long as people have thought about mathematics,” said Andrew Sills of Georgia Southern University.
The first mathematician to study partitions systematically was Leonhard Euler in the 18th century. He proved the very first partition identity: that for any integer (say, 4), the number of partitions whose parts are all odd (two partitions in this case: 3 + 1 and 1 + 1 + 1 + 1) is equal to the number of partitions whose parts are all distinct, meaning there are no repetitions among them (4 and 3 + 1).
MacMahon saw that the two Rogers-Ramanujan identities could be interpreted in a similar way. (The German mathematician Issai Schur, isolated due to World War I, independently discovered the identities and came to the same conclusion.) The sum side of the first Rogers-Ramanujan identity counts the number of partitions of a given integer that don’t have any duplicated or consecutive parts. (For the number 4, there are two: 4 and 3 + 1.) The product side counts the number of partitions whose parts all leave a remainder of 1 or 4 when divided by 5 (4 and 1 + 1 + 1 + 1). For any integer, the number of partitions satisfying each condition will always be equal.
This is a very weird fact. It’s mysterious,” said Shashank Kanade of the University of Denver. “I mean, where did the 5 come from?”
For much of the 20th century, mathematicians would delight in thinking about the strange hidden phenomena that Ramanujan had unearthed. During World War II, for instance, the physicist Freeman Dyson wrote that he “kept sane by wandering in Ramanujan’s garden.”
